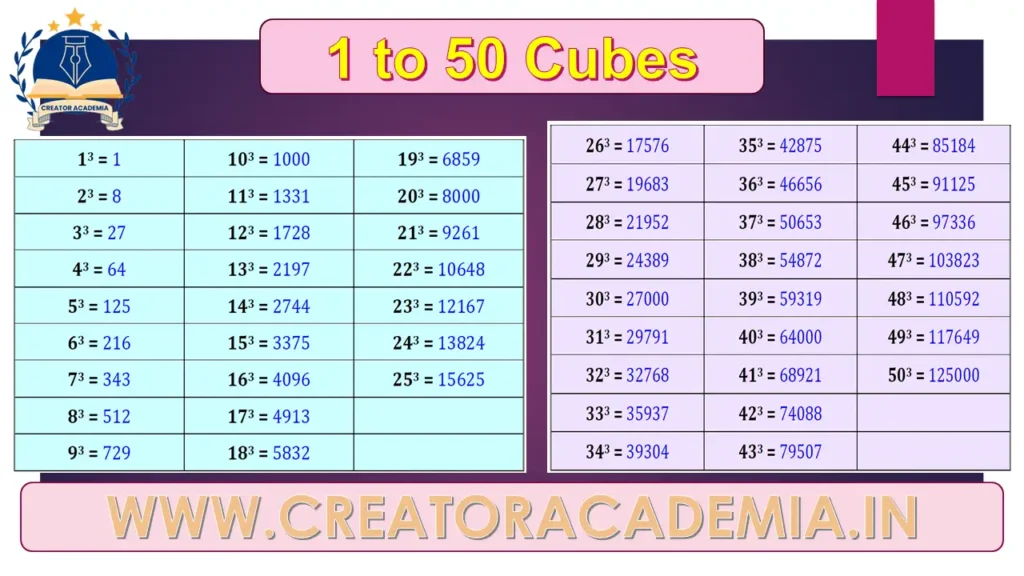
1 to 50 Cubes

Cubes are an important concept in mathematics. A cube of a number means multiplying the number by itself three times. It is used in many math problems, formulas, and real-life applications.
For example:
2³ = 2 × 2 × 2 = 8
7³ = 7 × 7 × 7 = 343

In this post, we will see the cubes of numbers from 1 to 50.

What is a Cube?
The cube of a number means multiplying the number by itself three times.
In short, Cube of a number = Number × Number × Number.
Example:

• Cube of 2 = 2 × 2 × 2 = 8
• Cube of 4 = 4 × 4 × 4 = 64
• Cube of 5 = 5 × 5 × 5 = 125

List of Cubes from 1 to 50:

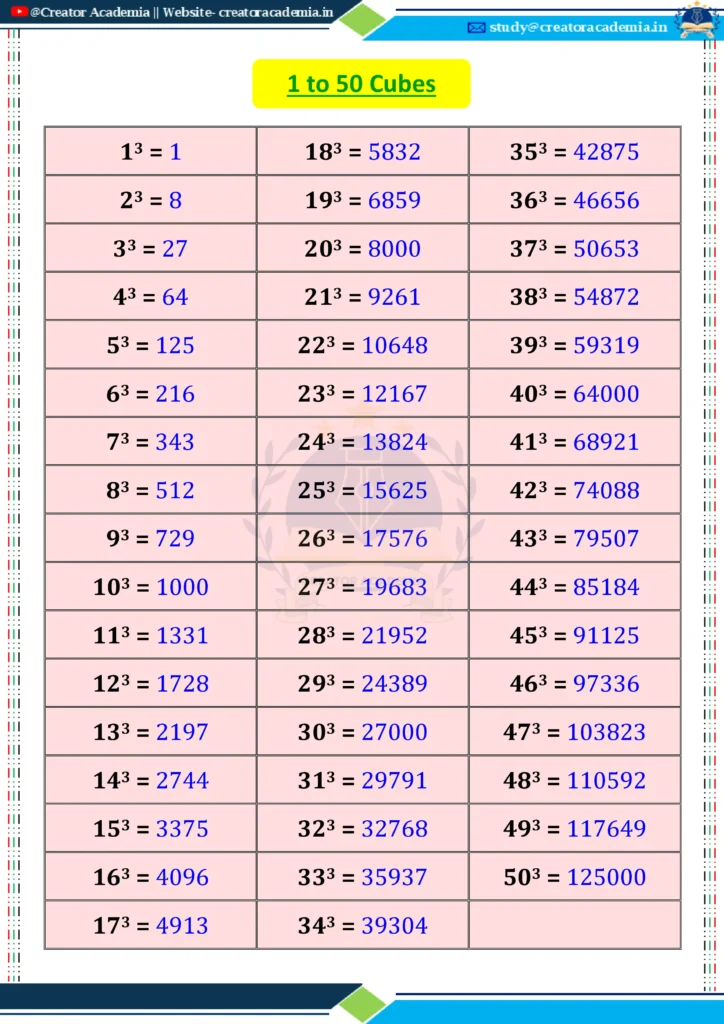
Download the PDF of 1 to 50 Cubes from the link given below.

Why Should You Learn Cubes from 1 to 50?

Today, especially in competitive exams, fast calculations are very important. Whether you are preparing for SSC, Bank, Railways, Defence, or any other exam, knowing cubes and cube roots is very helpful.

Benefits of Learning Cubes:

• Fast Calculations: Improves speed in multiplication problems.
• Exam Preparation: Useful for SSC, Banking, Railway, UPSC, and other exams.
• Algebra & Geometry: Many formulas involve cubes.
• Cube Roots: Helps in solving cube roots easily.
• Confidence: Strong basics improve overall math performance.

Tips to Learn Cubes Easily

• Practice daily: Regular revision makes it easier to remember.
• Break into Sets: First learn 1–10, then 11–20, and so on.
• Use Patterns: Cubes follow patterns like square numbers.
• Visual Method: Think of cubes as the volume of a cube (length × width × height).
• Flashcards: One side = number, other side = cube.
• Write and revise: Write cubes regularly to improve memory.

Short Tricks to Remember Cubes Quickly

Here are some short tricks to help you learn and remember cubes quickly and easily:

1. Cube of a Number = Number × Number × Number
First, always remember the basic formula:
Cube of n = n × n × n

• Example:
  • 3³ → 3 × 3 × 3 = 27
  • 8³ → 8 × 8 × 8 = 512

2. Last Digit Pattern Trick
👉 Trick: Cubes have unique last digits based on the last digit of the base number.
Numbers ending in 1 → Cube ends in 1 (e.g., 11³ = 1331)
Numbers ending in 2 → Cube ends in 8 (e.g., 2³ = 8)
Numbers ending in 3 → Cube ends in 7
Numbers ending in 4 → Cube ends in 4
Numbers ending in 5 → Cube ends in 5
Numbers ending in 6 → Cube ends in 6
Numbers ending in 7 → Cube ends in 3
Numbers ending in 8 → Cube ends in 2
Numbers ending in 9 → Cube ends in 9
Numbers ending in 0 → Cube ends in 0

• Example:
  • If n ends in 7 → n³ ends in 3
  • So, 17³ ends in 3

🧠 Use this trick to guess cube values in MCQs quickly.

3. Multiply and Add Method for Cubes
If you know the cube of a number, you can find the next cube quickly.
👉 Trick: (n + 1)³ = n³ + 3n² + 3n + 1

• Example:
  • 3³ = 27
  • 4³ = 3³ + (3×3²) + (3×3) + 1 = 27 + 27 + 9 + 1 = 64

4. Cube of Numbers Ending in 5
👉 Trick: For numbers ending in 5, use: (10a + 5)³ = 1000a³ + 1500a² + 750a + 125

• Example:
  • 15³ = (10×1 + 5)³ = 1000×1 + 1500×1 + 750×1 + 125 = 3375

5. Algebra Trick: (a + b)³
Use the identity:
👉 Trick: (a + b)³ = a³ + 3a²b + 3ab² + b³

• Example:
  • 12³ = (10 + 2)³ = 1000 + 3×100×2 + 3×10×4 + 8 = 1000 + 600 + 120 + 8 = 1728

6. Difference of Cubes Formula
👉 Trick: a³ – b³ = (a – b)(a² + ab + b²)

• Example:
  • Find 7³ using 8³:
    • 8³ = 512
    • 7³ = 8³ – (8 – 7)(8² + 8×7 + 7²) = 512 – 1(64 + 56 + 49) = 512 – 169 = 343

7. Cube of Even Numbers Pattern
👉 Trick: Even numbers’ cubes are always even.
They follow a doubling pattern.

• Example:
  • 2³ = 8
  • 4³ = 64
  • 6³ = 216

(Notice how rapidly the cube increases)

8. Cube of Odd Numbers Pattern
👉 Trick: Odd numbers’ cubes are always odd.
Perfect for spotting cube values in options.

• Example:
  • 1³ = 1
  • 3³ = 27
  • 5³ = 125
  • 7³ = 343

9. Perfect Cubes You Should Memorize
👉 Trick: Learn cubes of numbers 1 to 20 by heart—they are most frequently used.

• Example:
  • 13³ = 2197
  • 14³ = 2744
  • 15³ = 3375

(Practice these regularly)

10. Difference Between Cubes Increases Fast
👉 Trick: The difference between two consecutive cubes increases quickly.

• Example:
  • 2³ = 8
  • 3³ = 27 → Difference = 19
  • 4³ = 64 → Difference = 37
  • 5³ = 125 → Difference = 61

(Difference pattern = 19, 37, 61, …)

11. Break and Calculate (Use Mental Math)

👉 Trick: Use approximate values and mental math to break the cube into parts.

• Example:
  • Find 21³
    • = (20 + 1)³ = 8000 + 3×400×1 + 3×20×1 + 1 = 8000 + 1200 + 60 + 1 = 9261

Easy Tricks to Remember Cubes

If you feel scared about remembering so many cubes, don’t worry! Here are some easy tricks that can help you:

👉Trick 1: Memorize Small Numbers First
Cubes from 1 to 10 are very simple. With regular practice, you can easily memorize them.
Examples:
2³ = 8
3³ = 27
4³ = 64
5³ = 125

👉Trick 2: Understand the Rule
If the number is even, its cube will also be even.
If the number is odd, its cube will also be odd.
Examples:
2³ = 8 (even)
3³ = 27 (odd)

👉Trick 3: Break Big Numbers (Use Algebra)
(a + b)³ = a³ + 3a²b + 3ab² + b³
For example,
11³ = (10 + 1)³
= 1000 + 3×100×1 + 3×10×1 + 1
= 1000 + 300 + 30 + 1 = 1331

👉Trick 4: Look for Patterns
1³ = 1
11³ = 1331
21³ = 9261
There are interesting patterns in numbers like these. Recognizing patterns can help you memorize cubes faster.

👉Trick 5: Practice daily
Spend just 5-10 minutes a day writing and speaking cubes aloud. Daily practice will fix them in your mind very quickly.

Some Fun Facts About Cubes

1. Cubes don’t always end with the same digit.
Examples:
2³ = 8 → ends with 8
3³ = 27 → ends with 7

2. A cube of a positive number is always positive.

3. The difference between cubes of two consecutive numbers is large.
Examples:
2³ = 8 and 3³ = 27, Difference = 19
3³ = 27 and 4³ = 64, Difference = 37

4. Cubes are also used in Geometry to calculate the Volume of cube-shaped objects.

Uses of Cubes in Real Life

• Volume Calculation: Volume of a cube = side × side × side.
• Physics: Cubes are used in velocity and force formulas.
• Banking & Finance: Compound interest formulas use cubes.
• Computer Science: Algorithms sometimes involve cubes.
• Construction: Measurements and dimensions often use cube values.

Final Tips

• Practice Daily: Spend 5–10 minutes daily.
• Group numbers: Group numbers and learn in sets.
• Use Flashcards: Write the number on one side and its cube on the other.
• Challenge Yourself: Try to say cubes of random numbers in 10 seconds.
• Use mobile apps, games, or sticky notes.
• Teach your friends: Teaching helps you remember better.

Conclusion

Learning cubes from 1 to 50 helps in exams, faster calculation, and understanding advanced math topics. If you practice daily and use smart tricks, you will be able to remember all cubes easily. Start today and build your confidence in maths!

Some Important Links
Download 1 to 50 Cubes PDF	Click Here

If you are satisfied with our website creatoracademia.in, Please like and share with more people.
Join Telegram Channel	Join Now
Join WhatsApp Group for PDF	Join Now
For any Query and Feedback, Contact Us at – study@icreatoracademia.in.